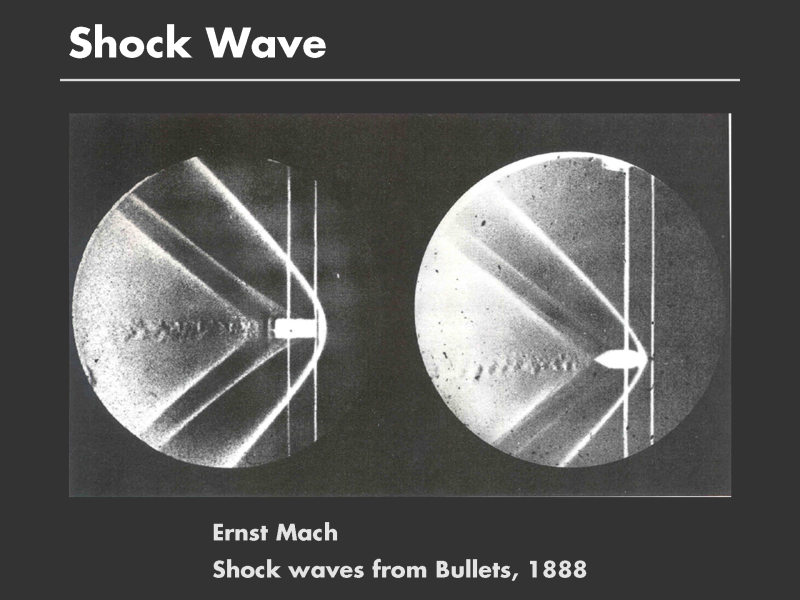
Here are a pair of images from a historic set of experiments undertaken by the German physicist and philosopher Ernst Mach (1838-1916), one of the most famous scientists of the last century.
Mach was interested in the pressure waves produced by a projectile moving faster than the speed of sound. Mach is often remembered because he defined the Mach Number, the ratio of the projectile speed to the speed of sound.
Mach showed:
- that sharper bullets produce less turbulence, and hence less drag, than blunt bullets. Comparing the two pictures, you can see the wider wake behind the blunt bullet on the left compared to the sharp bullet on the right.
- that there are two shockwaves (and hence two sonic booms) when a projectile reaches supersonic velocities. Notice the two shocks, one emanating from the front and the other from the back of the projectile.
These images were taken using the Schlieren technique which was developed by August Toepfer. The technique is based on two physical principles. First, the index of refraction varies as a function of the density of the medium. Second, when the index of refraction varies, light is refracted in the direction of the gradient. This same physics underlies mirages, where light is bent because the index of refraction changes with temperature. The Schlieren apparatus blocks un-refracted light, emphasizing the refracted light. (See http://www.rit.edu/~andpph/text-schlieren.html for additional details).
The pressure waves behind the projectile cause variations in density, Mach hypothesized that the Schlieren technique could be used to visualize these pressure waves. He added a camera and a sparking mechanism to trigger the exposure when the bullet was in view.
The brightest regions in the photograph are the shockwaves. A shockwave is formed when the pressure wavefront collapses on itself. This collapse, or singularity, causes extreme changes in density, This mathematical singularity is what defines a shockwave. A photograph taken using Schlieren technique, although clearly an example of photorealism, actually illustrates the very abstract mathematical property that causes the phenemenon..
Reference:
[1] p. 178-180, Beauty of Another Order: Photography in Science, Ed. Ann Thomas