

Next: Collections of Element
Up: Warping
Previous: Individual Feature Elements
As in the 2D morphing system of [2], the animator
identifies two corresponding features in 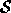 and
and 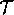 , by
defining a pair of elements
, by
defining a pair of elements 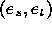 . These features
should be transformed to one another during the morph. Such a
transformation requires that the feature of
. These features
should be transformed to one another during the morph. Such a
transformation requires that the feature of 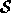 be moved,
turned, and stretched to match respectively the position, orientation,
and size of the corresponding feature of
be moved,
turned, and stretched to match respectively the position, orientation,
and size of the corresponding feature of 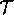 . Consequently, for
each frame of the morph, our warp should generate a volume
. Consequently, for
each frame of the morph, our warp should generate a volume 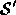 from
from 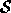 with the following property: the feature of
with the following property: the feature of 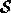 should possess an intermediate position, orientation and size in
should possess an intermediate position, orientation and size in
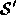 . This is achieved by computing the warp in two steps:
. This is achieved by computing the warp in two steps:
- Interpolation:
- We interpolate the local coordinate
systems
 and scaling factors of elements
and scaling factors of elements 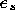 and
and
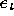 to produce an interpolated element
to produce an interpolated element 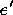 . This
element encodes the spatial configuration of the feature in
. This
element encodes the spatial configuration of the feature in
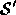 .
.
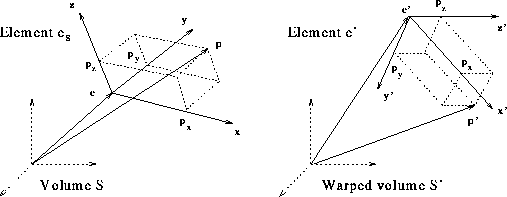
Figure 3: Single element warp. In order to find the point 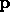 in
volume
in
volume 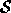 that corresponds to
that corresponds to 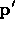 in
in 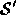 , we
first find the coordinates
, we
first find the coordinates 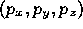 of
of 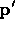 in the scaled
local system of element
in the scaled
local system of element 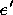 ;
; 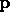 is then the point with
coordinates
is then the point with
coordinates 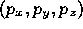 in the scaled local system of element
in the scaled local system of element
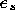 . To simplify the figure, we have assumed unity scaling
factors for all elements.
. To simplify the figure, we have assumed unity scaling
factors for all elements.
- Inverse mapping:
- For every point in
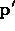 of
of 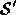 ,
we find the corresponding point
,
we find the corresponding point 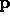 in
in 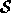 in two simple
steps (see figure 3): (i) We find the coordinates of
in two simple
steps (see figure 3): (i) We find the coordinates of
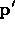 in the scaled local system of element
in the scaled local system of element 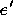 by
by

(ii) 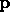 is the point with coordinates
is the point with coordinates 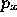 ,
, 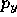 and
and 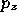 in
the scaled local system of element
in
the scaled local system of element 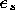 , i.e. the point
, i.e. the point
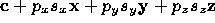 .
.
Last update: 11 May 1995 by Apostolos "Toli" Leriostolis@cs.stanford.edu
 and
and  , by
defining a pair of elements
, by
defining a pair of elements  . These features
should be transformed to one another during the morph. Such a
transformation requires that the feature of
. These features
should be transformed to one another during the morph. Such a
transformation requires that the feature of 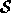 be moved,
turned, and stretched to match respectively the position, orientation,
and size of the corresponding feature of
be moved,
turned, and stretched to match respectively the position, orientation,
and size of the corresponding feature of 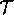 . Consequently, for
each frame of the morph, our warp should generate a volume
. Consequently, for
each frame of the morph, our warp should generate a volume 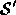 from
from 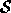 with the following property: the feature of
with the following property: the feature of 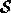 should possess an intermediate position, orientation and size in
should possess an intermediate position, orientation and size in
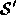 . This is achieved by computing the warp in two steps:
. This is achieved by computing the warp in two steps:
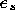 and
and
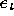 to produce an interpolated element
to produce an interpolated element 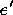 . This
element encodes the spatial configuration of the feature in
. This
element encodes the spatial configuration of the feature in
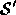 .
.

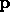 in
volume
in
volume 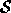 that corresponds to
that corresponds to 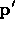 in
in 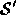 , we
first find the coordinates
, we
first find the coordinates 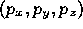 of
of 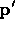 in the scaled
local system of element
in the scaled
local system of element 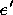 ;
; 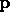 is then the point with
coordinates
is then the point with
coordinates 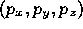 in the scaled local system of element
in the scaled local system of element
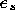 . To simplify the figure, we have assumed unity scaling
factors for all elements.
. To simplify the figure, we have assumed unity scaling
factors for all elements.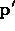 of
of 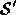 ,
we find the corresponding point
,
we find the corresponding point 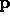 in
in 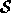 in two simple
steps (see figure 3): (i) We find the coordinates of
in two simple
steps (see figure 3): (i) We find the coordinates of
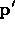 in the scaled local system of element
in the scaled local system of element 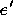 by
by

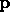 is the point with coordinates
is the point with coordinates 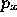 ,
, 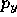 and
and 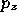 in
the scaled local system of element
in
the scaled local system of element 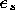 , i.e. the point
, i.e. the point
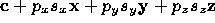 .
.