

Next: User Interface
Up: Warping
Previous: Element Pairs
In extending the warping algorithm of the previous paragraph to
multiple element pairs, we adhere to the intuitive mental model of
magnetic sculpting used in [2]. Each pair of elements
defines a field that extends throughout the volume. A collection of
element pairs defines a collection of fields, all of which
influence each point in the volume. We therefore use a weighted
averaging scheme to determine the point 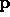 in
in 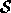 that
corresponds to each point
that
corresponds to each point 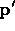 of
of 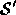 . That is, we first
compute to what point
. That is, we first
compute to what point 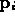 each element pair would map
each element pair would map
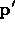 in the absence of all other pairs; then, we average the
in the absence of all other pairs; then, we average the
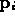 's using a weighting function that depends on the distance
of
's using a weighting function that depends on the distance
of 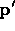 to the interpolated elements
to the interpolated elements 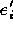 .
.
Our weighting scheme uses an inverse square law: 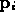 is
weighted by
is
weighted by 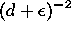 where d is the distance of
where d is the distance of
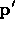 from the element
from the element 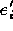 ;
;  is a small
constant used to avoid division by zero.
is a small
constant used to avoid division by zero. The type of element
The type of element 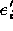 determines how d is calculated:
determines how d is calculated:
- Points:
- d is the distance between
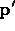 and the origin
and the origin
 of the local coordinate system of element
of the local coordinate system of element 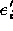 .
This definition is identical to [21].
.
This definition is identical to [21].
- Segments:
- The element is treated as a line segment centered at
the origin
 , aligned with the local x-axis and having
length
, aligned with the local x-axis and having
length 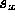 ; d is the distance of
; d is the distance of 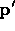 from this line
segment. This definition is identical to [2].
from this line
segment. This definition is identical to [2].
- Rectangles:
- Rectangles have the same center and x extent as
segments, but also extend into a second dimension, having width
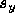 along the local y-axis. d is zero if
along the local y-axis. d is zero if 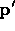 is on
the rectangle, otherwise it is the distance of
is on
the rectangle, otherwise it is the distance of 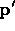 from the
rectangle. This definition extends segments to area elements.
from the
rectangle. This definition extends segments to area elements.
- Boxes:
- Boxes add depth to rectangles, thus extending for
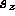 units along the local z-axis. d is zero if
units along the local z-axis. d is zero if 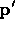 is within the box, otherwise it is the distance of
is within the box, otherwise it is the distance of 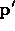 from the
box's surface.
from the
box's surface.
The reader will notice that the point, segment, and rectangle element
types are redundant, as far as the mathematical formulation of our
warp is concerned. However, a variety of element types maintains best
the intuitive conceptual analogy to magnetic sculpting.


Next: User Interface
Up: Warping
Previous: Element Pairs
Last update: 11 May 1995 by Apostolos "Toli" Leriostolis@cs.stanford.edu
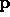 in
in 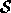 that
corresponds to each point
that
corresponds to each point 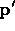 of
of 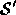 . That is, we first
compute to what point
. That is, we first
compute to what point 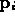 each element pair would map
each element pair would map
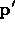 in the absence of all other pairs; then, we average the
in the absence of all other pairs; then, we average the
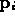 's using a weighting function that depends on the distance
of
's using a weighting function that depends on the distance
of 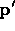 to the interpolated elements
to the interpolated elements 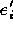 .
.
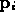 is
weighted by
is
weighted by 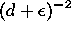 where d is the distance of
where d is the distance of
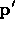 from the element
from the element 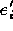 ;
;  is a small
constant used to avoid division by zero.
is a small
constant used to avoid division by zero.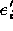 determines how d is calculated:
determines how d is calculated:
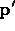 and the origin
and the origin
 of the local coordinate system of element
of the local coordinate system of element 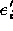 .
This definition is identical to [21].
.
This definition is identical to [21].
 , aligned with the local x-axis and having
length
, aligned with the local x-axis and having
length 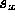 ; d is the distance of
; d is the distance of 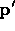 from this line
segment. This definition is identical to [2].
from this line
segment. This definition is identical to [2].
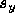 along the local y-axis. d is zero if
along the local y-axis. d is zero if 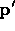 is on
the rectangle, otherwise it is the distance of
is on
the rectangle, otherwise it is the distance of 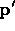 from the
rectangle. This definition extends segments to area elements.
from the
rectangle. This definition extends segments to area elements.
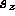 units along the local z-axis. d is zero if
units along the local z-axis. d is zero if 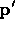 is within the box, otherwise it is the distance of
is within the box, otherwise it is the distance of 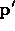 from the
box's surface.
from the
box's surface.