Grader: Kekoa Proudfoot
Recall Bresenhan's algorithm to draw a line (we've slightly simplified the procedure):
line(int x, int y, int n, int a, int b, int c)
{
int i;
int e = a * x + b * y + c;
for (i = 0; i < n; i++) {
point(x, y);
e += a;
x += 1;
if (e < 0) {
y += 1;
e += b;
}
}
}
This procedure works for lines drawn in the first octant (slopes less than 45 degrees). It also assumes that the orientation of the line has been chosen so that vector (a,b) perpendicular to the line points upward and to the left.
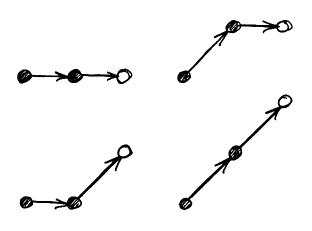
One clever optimization that can be performed is to take two steps every time through the loop, in the process drawing two pixels instead of one. What are the possible two-step pixel patterns that may occur?
Answer:
Remarks:
This question was about two-step pixel patterns. There are four possible patterns; what distinguishes each pattern from the next is, for each of the two pixels, whether or not the step after that pixel goes straight to the right, or up and to the right.
Grading:
5 points were awarded to students who demonstrated, in their answer to question 5A, that they recognized that all four cases were possible.
4 points were awarded to students who only answered that three cases were possible. Usually, these students incorrectly eliminated the the up-up case as a case that could not occur.
3 points were awarded to students that only reported two cases. A majority of these students focused on the pixels themselves and not on the steps taken after the pixels.
1 point was awarded to students that otherwise made a reasonable attempt at an answer.
0 points were awarded to students who did not make a reasonable attempt at an answer.
How would you modify the inner loop to distinguish between these cases? For simplicity, assume that n is even. Your changes should be as efficient as possible.
Answer:
line(int x, int y, int n, int a, int b, int c)
{
int i;
int e = a * x + b * y + c;
int aa = a + a;
int bb = b + b;
if (-b - aa >= 0) {
for (i = 0; i < n; i += 2) {
if (e < -a) {
if (e < -b - aa) {
point(x++, y++);
point(x++, y++);
e += aa + bb;
}
else {
point(x++, y++);
point(x++, y);
e += aa + b;
}
else {
point(x++, y);
point(x++, y++);
e += aa + b;
}
}
}
else {
for (i = 0; i < n; i += 2) {
if (e < -a) {
point(x++, y++);
point(x++, y);
e += aa + b;
}
else {
if (e < -aa) {
point(x++, y);
point(x++, y++);
e += aa + b;
}
else {
point(x++, y);
point(x++, y);
e += aa;
}
}
}
}
}
Remarks:
The most important aspect of question 5B was finding the correct conditions on e to distinguish the four cases efficiently. The correct conditions were:
Condition Case 0 <= e < -b - 2a up, up -b - 2a <= e < -a up, right -a <= e < -2a right, up -2a <= e < 1 right, right Up denotes a step up and to the right, right denotes a step to the right only.
Note that, because of the slope of the line, a < 0, b > 0, and b > -a. Also note that 0 <= e < b.
A secondary aspect of this question was to notice that the "right, right" case is not possible if the "up, up" case is possible, and vice-versa. Which case is possible depends on whether or not -b - 2a < 0. If -b - 2a < 0, then b > -2a, and the line is mostly horizontal, elimintaing the "up, up" case; likewise, if -b - 2a >= 0, then b <= -2a, the line is closer to 45° than to horizontal, eliminating the "right, right" case. You can also see that this is the case by looking at how these relationships between b and -2a affect the "up, up" case and the "right, right" case given that 0 <= e < b.
The answer shown above takes into account both aspects of the problem, and illustrates the minimum required for the full 15 points, under the assumption that the compiler would handle the rest of the optimizations, including loop invariance and common subexpression elimination.
Because the final point was hard to get, here is code that would have earned 14 points:
line(int x, int y, int n, int a, int b, int c)
{
int i;
int e = a * x + b * y + c;
int aa = a + a;
int bb = b + b;
for (i = 0; i < n; i += 2) {
if (e < -a) {
if (e < -b - aa) {
point(x++, y++);
point(x++, y++);
e += aa + bb;
}
else {
point(x++, y++);
point(x++, y);
e += aa + b;
}
else {
if (e < -aa) {
point(x++, y);
point(x++, y++);
e += aa + b;
}
else {
point(x++, y);
point(x++, y);
e += aa;
}
}
}
}
Students that first offset e by 2a, then used -b, a, and 0 as boundary values were given credit for correctly determining the conditions on e.
Students that did not determine the correct boundary values for e, but specifically noted which sections of code applied to which of the four cases, were given points for making it clear that they knew which case was which.
Some students approached the problem by simply unrolling the loop once. We awarded only half credit for this solution.
Some students unrolled the loop once and transformed their code to make it more efficient, but never got to the point where they made it clear that they knew the boundary conditions on e. Other students wrote code from scratch, but never discovered the boundary conditions on e. We awarded the same number of points to these students, which, depending on the level of optimizations, was a few points more than we gave to students who simply unrolled the loop once.
Grading:
14 points were awarded to students who calculated or described the boundary conditions on e or who explicitly expressed these boundary conditions in their code. Specifically, I was looking for some variation of the -b - 2a, -a, and -2a conditions.
13 points were awarded to students who did not calculate the boundary conditions on e or express them in their code, but who instead labelled which sections of code corresponded to each of the four cases.
12 points were awarded to students who thought that only three cases existed and went ahead and calculated or described the boundary conditions on e or explicitly expressed these boundary conditions in their code, but only for the three cases.
10 points were awarded to students who did not calculate or describe the boundary conditions on e but who otherwise managed to write reasonably efficient code.
9 points were awarded to students who did not calculate or describe the boundary conditions on e but did manage to write code that looked only slightly more efficient than unrolled code.
8 points were awarded to students who simply unrolled the loop.
5-7 points were awarded to students who only handled two cases in their code, or who otherwise made an attempt to get things to work with only two cases.
3 points were awarded to students who otherwise made a reasonable attempt at writing code that made sense.
0-1 points were awarded to students who didn't make a reasonable attempt to solve the problem.
1 additional point was awarded for the observation that the "up, up" case and the "right, right" case could not both appear within a single line.
1 point was deducted for inefficient code if your base score was higher than 12 points.
1-2 points were deducted for various small mistakes, such as a flipped sign, a flipped comparison operator, a misplaced preincrement or postincrement, or a dropped first pixel.